The discovery of irrational numbers came from a sect
Was a mathematician drowned by members of a strange cult? Many myths and legends revolve around the history of irrational numbers.
He was punished with death for his discovery of irrational numbers - at least that is the legend surrounding the ancient scholar Hippasos of Metapont. What actually happened in the 5th century BC is still unclear to this day.
Numbers beyond fractions
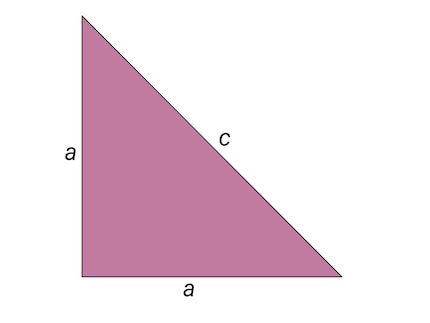
The proof presented by Hippasus (or another Pythagorean) is most easily illustrated with an isosceles and right-angled triangle, even though the original proof was probably performed on a different geometric figure (probably the pentagon). The two cathets of length a in an isosceles right-angled triangle therefore form a right angle, opposite which lies the hypotenuse of length c.
Such a triangle has a fixed aspect ratio a⁄c. If both a and c are rational numbers, the lengths of the sides of the triangle can be chosen so that a and c correspond to the smallest possible natural numbers (i.e. they have no common divisors). For example, if the aspect ratio were ⅔, you would choose a = 2 and c = 3. This means: Assuming that the lengths of the triangle correspond to rational numbers, a and c are integers and have no common divisors.
A proof of contradiction
Hippasos used this fact to create a contradiction - and thus prove that the original assumption must be wrong. Firstly, he used the Pythagorean theorem to express the length of the hypotenuse c as a function of the two cathets a: 2a2 = c2. Since a and c are integers, it follows from the previous equation that c2 must be an even number. Accordingly, c is also divisible by two: c = 2n, where n is a natural number.
Substituting c = 2n into the original equation results in: 2a2 = (2n)2 = 4n2. The two can be reduced on both sides, which gives the following result: a2 = 2n2. Since a is also an integer, it follows that a2 and therefore also a are even numbers. However, this contradicts the original assumption; because if a and c are both even, they cannot be divisors.
This allowed Hippasos to conclude that the aspect ratio of an isosceles right-angled triangle a⁄c cannot correspond to a rational number. In other words, there are numbers that cannot be represented as the ratio of two integer values. For example, if you choose the lengths of the two sides of the triangle a = 1, then c = √2. And as we know today, √2 is an irrational number. Its decimal places continue indefinitely without ever repeating themselves.
From today's perspective, the existence of irrational values does not seem too surprising because we are confronted with this fact at a very young age. It is difficult to assess what effect such a realisation must have had around 2500 years ago. In any case, it must have turned the mathematical world view upside down. No wonder there are so many myths and legends about this discovery.
Spectrum of science
We are partners of Spektrum der Wissenschaft and want to make well-founded information more accessible to you. Follow Spektrum der Wissenschaft if you like the articles.
Original article on Spektrum.deExperts from science and research report on the latest findings in their fields – competent, authentic and comprehensible.
From the latest iPhone to the return of 80s fashion. The editorial team will help you make sense of it all.
Show all