© raland / stock.adobe.com (extrait) Les pythagoriciens étaient considérés comme une sorte de secte - leurs membres étaient persécutés et tués.

Nouveautés + tendances

La découverte des nombres irrationnels est venue d'une secte

5/6/2024

Traduction : traduction automatique

Un mathématicien a-t-il été noyé par les membres d'un étrange culte ? De nombreux mythes et légendes tournent autour de l'histoire des nombres irrationnels.

Pour avoir découvert les nombres irrationnels, il a été puni de mort - c'est du moins la légende qui entoure le savant antique Hippasos de Métaponte. Ce qui s'est réellement passé au 5e siècle avant notre ère n'est toujours pas clair aujourd'hui.

Il semble qu'Hippasos ait fait partie des pythagoriciens, une sorte de secte qui s'occupait entre autres de mathématiques et de mystique des nombres. L'un des éléments clés de leur enseignement concernait les rapports numériques harmoniques, qui comprenaient des fractions de nombres entiers. Les nombres naturels et rationnels permettaient à l'époque de décrire le monde entier. Mais lorsqu'Hippasos examina les rapports de longueur d'un pentagramme - le symbole des pythagoriciens - il se rendit compte que certaines longueurs de côtés ne pouvaient pas être exprimées sous forme de fractions

Il a ainsi fourni la première preuve documentée de l'existence de nombres irrationnels. Selon certaines histoires, les pythagoriciens lui en auraient voulu, car de tels nombres allaient à l'encontre de leur vision du monde. D'après d'autres interprétations, Hippasos aurait publié son résultat, violant ainsi les règles de confidentialité de la Confédération. Quoi qu'il en soit, Hippasos s'est apparemment noyé en mer après sa découverte. Il est parfois rapporté que les pythagoriciens l'auraient jeté d'un navire après qu'il les ait informés de sa découverte - ou bien que sa mort était un accident, mais que les pythagoriciens auraient considéré cela comme une punition de Dieu. Les interprétations actuelles estiment que rien de tout cela n'est vrai. Au contraire, la découverte d'Hippasos aurait déjà été reconnue à l'époque comme une percée mathématique dont les pythagoriciens étaient fiers - à condition que la preuve soit bien d'Hippasos. Car même cela n'est pas certain.

La seule chose dont on dispose est que les pythagoriciens ont prouvé l'incommensurabilité de certaines grandeurs, dont découle l'existence de nombres irrationnels. Les pythagoriciens eux-mêmes font l'objet de nombreuses histoires dont la véracité est souvent douteuse. La communauté a probablement été fondée dans le sud de l'Italie actuelle par Pythagore de Samos - le savant grec qui a donné son nom au célèbre théorème de Pythagore (bien qu'il ne soit pas certain qu'il ait réellement prouvé le théorème).

Les pythagoriciens rejetaient la richesse et menaient une vie végétarienne et ascétique. Ils croyaient en outre à la réincarnation, ce qui les distinguait du reste de la population de la Grèce antique. Outre les mathématiques, la communauté s'intéressait probablement à la philosophie et à la politique. Cependant, leur point de vue n'a pas été très apprécié et ils ont été persécutés : Plusieurs attentats ont été perpétrés contre la communauté ; quelques décennies après la mort de Pythagore, la confédération a complètement disparu.

Les nombres au-delà des fractions

Bien que beaucoup de choses autour des pythagoriciens restent mystérieuses, ils sont largement considérés comme les découvreurs des nombres irrationnels. Aujourd'hui, nous apprenons à l'école qu'il existe des valeurs qui ne peuvent pas être exprimées comme le quotient de deux nombres entiers. Mais cette découverte ne semble pas du tout naturelle : après tout, toutes les valeurs irrationnelles peuvent être approchées avec précision par des fractions - même si cela est plus difficile pour certains nombres irrationnels que pour d'autres.

La preuve apportée par Hippasos (ou un autre pythagoricien) peut être illustrée le plus simplement possible par un triangle isocèle et rectangle, même si la preuve originale a probablement été faite sur une autre figure géométrique (probablement le pentagone). Ainsi, les deux cathètes de longueur a dans un triangle isocèle rectangle forment un angle droit auquel est opposée l'hypoténuse de longueur c.

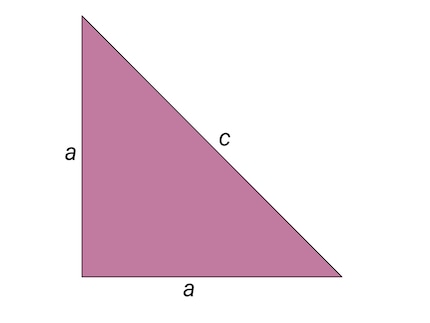
Triangle | L'existence des nombres irrationnels s'explique le mieux par un triangle isocèle rectangle.
Source : © Spektrum der Wissenschaft / Manon Bischoff (extrait)

Un tel triangle a un rapport de côtés a⁄c fixe. Si a et c sont tous deux des nombres rationnels, on peut choisir les longueurs des côtés du triangle de telle sorte que a et c correspondent aux plus petits nombres naturels possibles (ils n'ont donc pas de diviseurs communs). Par exemple, si le rapport des côtés était ⅔, on choisirait a = 2 et c = 3. Autrement dit, en supposant que les longueurs du triangle correspondent à des nombres rationnels, a et c sont des entiers et des diviseurs étrangers.

Une preuve de contradiction

Hippasos a utilisé ce fait pour créer une contradiction - et ainsi prouver que l'hypothèse initiale devait être fausse. Il a d'abord utilisé le théorème de Pythagore pour exprimer la longueur de l'hypoténuse c en fonction des deux cathètes a : 2a2 = c2. Comme a et c sont des nombres entiers, il découle de l'équation précédente que c2 doit être un nombre pair. Par conséquent, c est également divisible par deux : c = 2n, où n est un entier naturel.

En insérant c = 2n dans l'équation initiale, on obtient : 2a2 = (2n)2 = 4n2. Des deux côtés, on peut raccourcir le deux, ce qui donne le résultat suivant : a2 = 2n2. Comme a est également un nombre entier, il s'ensuit que a2 et donc a sont des nombres pairs. Mais cela va à l'encontre de l'hypothèse initiale, car si a et c sont tous deux pairs, ils ne peuvent pas être étrangers à des diviseurs.

Ainsi, Hippasos pouvait conclure que le rapport des côtés d'un triangle rectangle isocèle a⁄c ne pouvait correspondre à aucun nombre rationnel. En d'autres termes, il existe des nombres qui ne peuvent pas être représentés comme des rapports entre deux valeurs entières. Par exemple, si l'on choisit les longueurs des deux cathètes du triangle a = 1, alors c = √2. Et comme nous le savons aujourd'hui, √2 est un nombre irrationnel. Ses chiffres après la virgule se poursuivent indéfiniment sans jamais se répéter.

D'un point de vue actuel, l'existence de valeurs irrationnelles ne semble pas trop étonnante, car nous sommes confrontés à ce fait très jeunes. Il est difficile d'évaluer l'impact d'une telle découverte il y a environ 2500 ans. Elle a en tout cas dû bouleverser la vision mathématique du monde. Il n'est donc pas étonnant qu'il y ait tant de mythes et de légendes autour de cette découverte.

Spektrum der Wissenschaft

Nous sommes partenaires de Spectre des Sciences et souhaitons vous rendre les informations fondées plus accessibles. Suivez Spectre des Sciences si vous aimez ses articles.

Article original sur Spektrum.de

Photo d’en-tête : © raland / stock.adobe.com (extrait) Les pythagoriciens étaient considérés comme une sorte de secte - leurs membres étaient persécutés et tués.

Cet article plaît à 14 personne(s)

Spektrum der Wissenschaft

Wissenschaft aus erster Hand

dirdjaja@spektrum.de

Des experts de la science et de la recherche rendent compte des dernières découvertes dans leur domaine – de manière compétente, authentique et compréhensible.

Nouveautés + tendances

Du nouvel iPhone à la résurrection de la mode des années 80. La rédaction fait le tri.

Tout afficher

1 commentaire

later

Vos données. Votre choix.

Recherche

La découverte des nombres irrationnels est venue d'une secte

Les nombres au-delà des fractions

Une preuve de contradiction

Spektrum der Wissenschaft

1 commentaire

Top 10 catégories

Aller à

1 commentaire